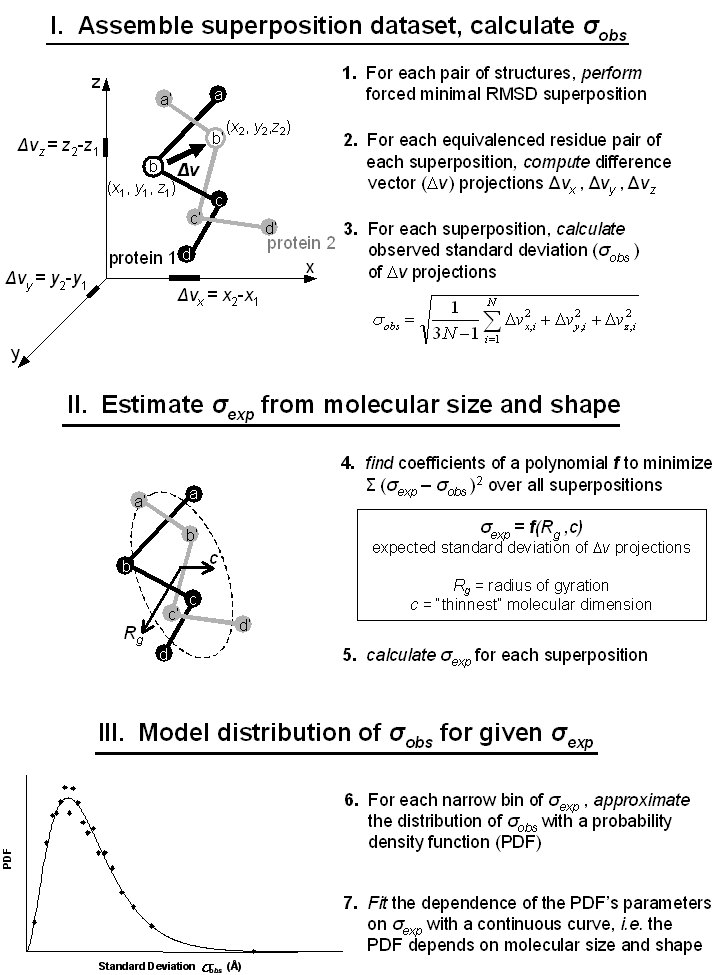
Random model of protein structure superposition. Two four-residue fragments of non-homologous protein chains are shown as spheres, representing CA atoms, connected by virtual bonds. One fragment, "protein 1", is colored black, the second, "protein 2", gray. Gapless equivalences of Cα atoms, depicted by, e.g. the labels b and b' in the figure, were forced regardless of structural similarity and a minimum RMSD superposition was performed. Such a forced superposition was termed a "random" superposition. Coordinate difference vector projections (DVPs) and their standard deviation, σ_obs, were computed from the random superposition. As an example, three projections Δv_{x, y, z} (short thick lines on the x, y, z axes) from one vector Δv (arrow) are indicated. This procedure was repeated for all pairs of fragments in the dataset (32,004 pairs). Then two size and shape parameters from each superposition, Rg (gyration radius) and c, were used in a singular value decomposition (SVD) generalized linear least squares fit to determine coefficients for a polynomial f. Polynomial f estimated the expected standard deviation of projections, σ_exp, given the size and shape of a superposition, and σ_exp was calculated for all random superpositions in the set. Finally, distributions of σ_obs for a narrow range of σ_exp (0.2Å increments) were extracted and approximated with a PDF (Nakagami distribution). Parameters for this PDF were therefore dependent on size and shape of the random superpositions contained within the narrow range of σ_exp. These parameters were subsequently fit to a continuous curve with σ_exp as the independent variable. The continuous curve allowed construction of a random model, and therefore estimation of a p-value, for a superposition of arbitrary size and shape. As explained in the text but not shown in the figure, PDF parameters describing a distribution of σ_obs simultaneously described the corresponding distribution of projections Δv_{x, y, z}, using a second PDF (Variance-Gamma distribution).