Target Categories in CASP9
Some targets are easy to predict, as they have very close templates among known structures, other targets are quite challenging. It is essential to evaluate predictions taking into account target difficulty, since performance of different algorithms depends on it. Grouping targets into categories of approximately the same prediction difficulty brings out the flavors of how each method deals with different target types.
In CASP9, targets were classified in two general categories: TBM (template-based modelling) and FM (Free Modelling), to reflect the method that was used to obtain models. Clearly, templates have something to do with it, like TBM assumes presence of templates by definition. Does FM assume absence of template by definition? we would say it is not. Traditionally, predictors thought about FM as 'hard'. FM, which is "free modelling", is a category where predictors are 'free' to do whatever they can, as they can't get is right anyway:). Then, how to define CASP9 category? It became clear with time that the best approach is to use a combination of various methods as what matters is the quality of the final prediction. Therefore, it is logical to group targets into categories by the prediction quality.
During CASP8 season, we developed a general approach which leads to a well-defined boundaries between categories coming out naturally from the data 1). For CSAP9, we applied very similar approach to define the target categories based on the quality of predictions. We resorted to a traditional model quality metric that stood the test of time – LGA GDT-TS scores. Targets for which domain-based evaluation is essential, as established by our analysis, were split into domains, and other targets remained as whole chains and were considered as single domain targets for evaluation purpose. This procedure resulted in 147 "domains" gathered from 116 targets. For each of these domains, we took GDT_TS score for the best server models, and calculated the median GDT_TS for above random models. Moreover, the rank of random model was recorded. Those two values were used to measure each target's difficulty.
We looked for naturally emerging clusters in these median GDT-TS scores and
ranks of random models and used Gaussian kernel density estimation. Gaussian kernel density estimator is a function
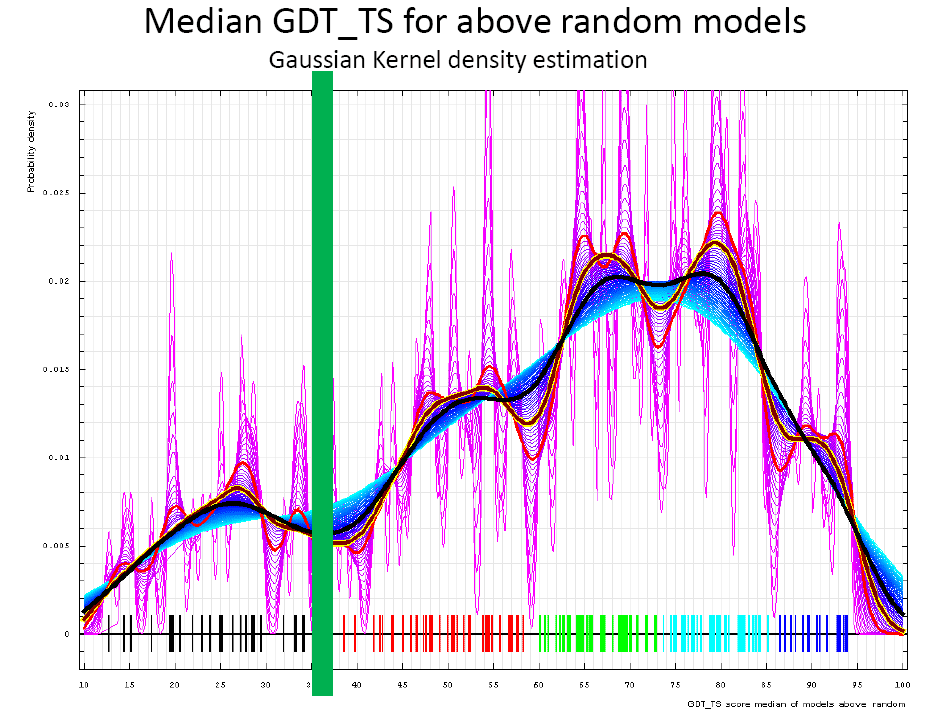
Domains:
Gaussian kernel density estimation of domain GDT-TS scores for the median best model GDT-TS
for above random models, plotted at various bandwidths (= standard deviations).
These median GDT-TS scores for domains are shown as a spectrum along the horizontal axis: each bar
represents a domain. The darkgreen bar indicates the reasonable bound, which partition target domains into tow categories.
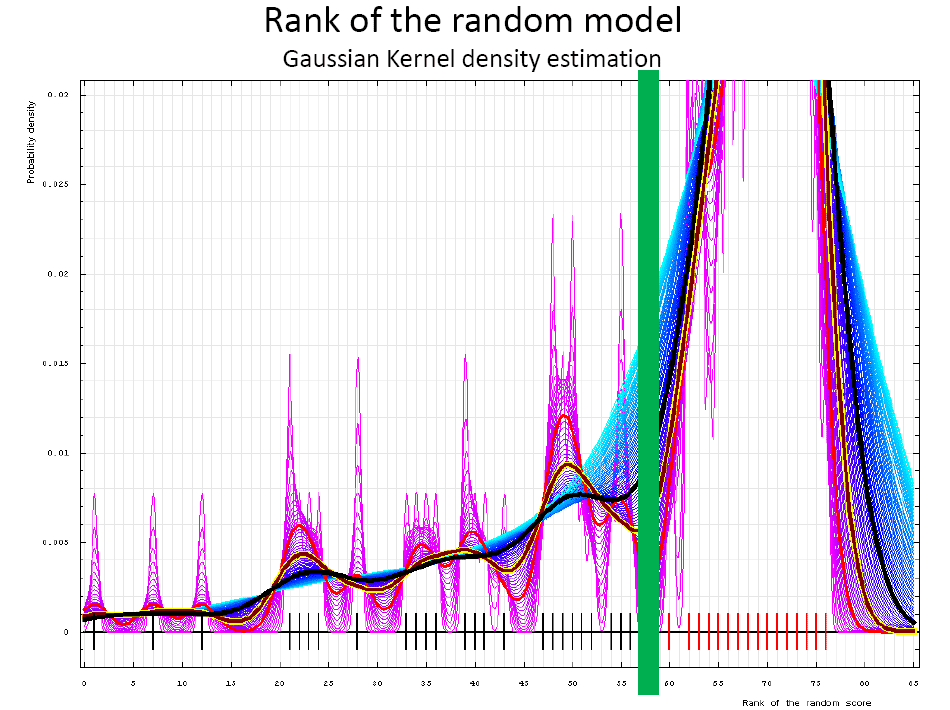
Domains:
Gaussian kernel density estimation of rank of random model, plotted at various bandwidths (= standard deviations).
These ranks of random models for domains are shown as a spectrum along the horizontal axis: each bar
represents a domain. The darkgreen bar indicates the reasonable bound, which partition target domains into tow categories.
We combine the median GDT_TS for above random model and rank of the random model, and plot 2D of these CASP9 category definition as below:
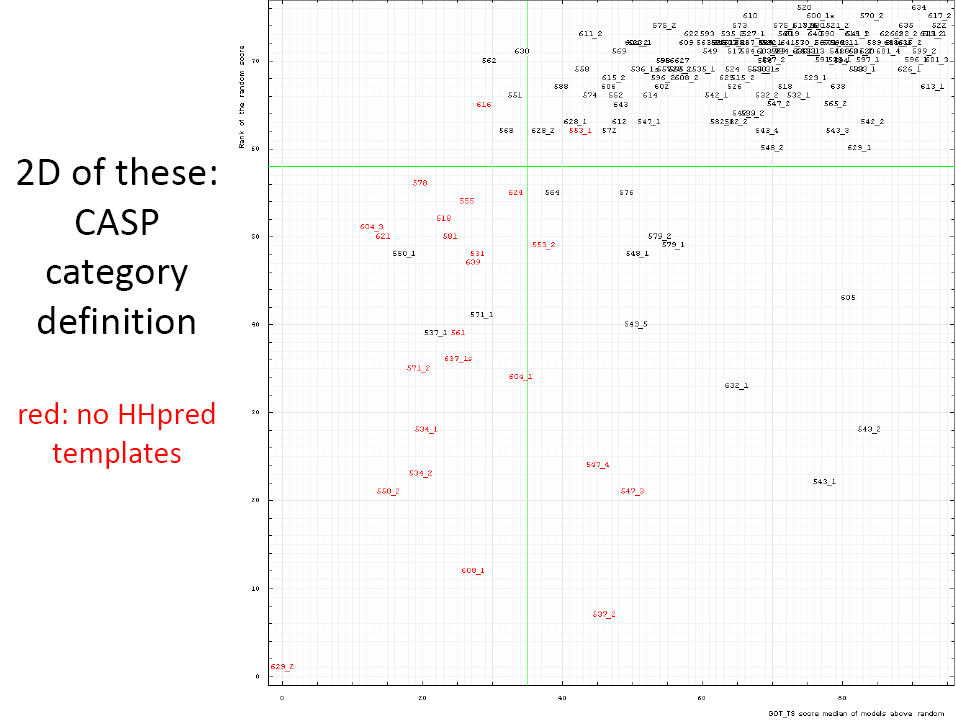
domains that do not have template available are colored in red
From the 2D plot of these CASP9 category definition, cleary, the domains located at the left lower cornor should go to the FM category. Except that, we also would like to take the domains that do not have template available as FM targets, which results in 30 FM targets in total.
